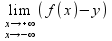36. Исследование функции с помощью производной. Асимптоты

Прямая y=kx+b называется наклонной асимптотой функции с бесконечной

областью определения при х→+∞(х→-∞)

если 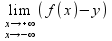=0 Прямая y=kx+b называется наклонной асимптотой

функции с бесконечной областью определения при х→+∞(х→-∞), если

расстояние от любой точки М(х,f(x)) графика функции до прямой стремится

к 0 при х→+∞(х→-∞).

Теорема. Необходимое и достаточное условие наклонных асимптот

Если функция f(x) определена и дифференцируема внутри окрестности

+∞(-∞) и выполняются равенства 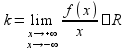и

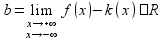
или (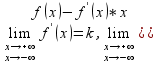, то прямая y=kx+b является

наклонной асимптотой

Замечание:

1.Если хотя бы один из пределов не существует или равен ∞, то наклонных

асимптот нет

2.Если k=0,то прямая y=b называется горизонтальной асимптотой.

Признак горизонтальной асимптоты

Y=b является горизонтальной асимптотой в том и только том случае

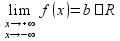
Прямая x=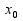 называется вертикальной асимптотой при

х→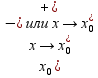, если 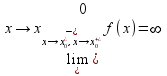, 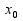является точкой разрыва

2 рода