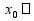35. Исследование функции с помощью производной. Нахождение точек перегиба.

Внутренняя точка области определения функции называется точкой перегиба, если

при переходе через эту точку функция меняется выпуклость на вогнутость или наоборот.

Теорема. Необходимое и достаточное условие точки перегиба.

Пусть функция f(х)определена на <a,b> и дифференцируема внутри него, тогда для того

чтобы внутренняя точка 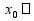<a,b> была точкой перегиба, необходимо и достаточно, чтобы

при переходе через эту точку, производная меняла возрастание на убывание .

Теорема. Необходимое условие точек перегиба

Пусть функция f определена на Х, 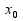-внутренняя точка Х и существует f''(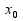) и 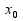-точка

перегиба, тогда f ''(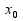)=0.

Теорема. Достаточное условие точки перегиба.

Пусть функция f определена на Х и дважды дифференцируема внутри него.

Пусть 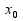-внутренняя точка области определения, тогда при переходе через

точку 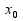f''(х) меняет свой знак, то 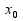является точкой перегиба.