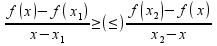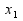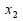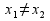33. Исследование функции с помощью производной. Определение выпуклости

и вогнутости функции. Неравенство выпуклости и вогнутости

Выпуклость, вогнутость

Лемма. Пусть 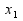,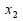-два произвольных числа ,

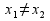тогда φ(λ)=(1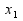-λ)+λ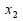 отображает [0,1] на [].

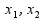Д-во.

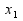φ(λ)=+λ()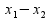

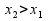
_{φ(λ)-линейная функция относительно λ, причем}

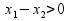, тогда φ(λ)-возрастающая функция.

φ(0)=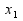 φ(1)=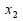,таким образом получаем, что

φ: [0,1] → [].

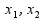Функция f(x) называется выпуклой(вогнутой)

на <a,b>,если ∀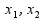∊<a,b>∀λ∊[0,1] выполняется неравенство

f(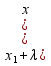)≥(≤)f(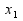)+λ(f))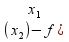

Теорема. Геометрический смысл выпуклости и вогнутости

Если функция выпукла(вогнута) на промежутке <a,b> ,

то любая дуга графика лежит не ниже(не выше) хорды,

соединяющей концы этой дуги.

Теорема. Неравенство выпуклости(вогнутости) из предыдущего

определения можно переписать в виде: