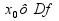 ,если
существует V(
,если
существует V(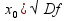 ,
на которой
,
на которой
32. Исследование функции с помощью производной. Экстремумы функции. Необходимые и достаточные условия экстремумов.
Точкой max(min) функции f(x) с областью определения Df
называется
точка
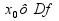 ,если
существует V(
,если
существует V(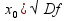 ,
на которой
,
на которой
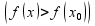
Геометрически точки max и min являются вершинами
выпуклости и вогнутости.
Точки max и min носят общее название точек экстремума
Теорема. Необходимое условие экстремума
Пусть
функция f(x)
дифференцируема на Х,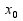 -точка
экстремума, тогда f’(x)=0.
-точка
экстремума, тогда f’(x)=0.
Д-во.
По т. Ферма.
Точки, в которых производная обращается в 0 называются стационарными.
Точки, в которых производная не существует или обращается в ∞ называются критическими.
Все они носят общее название подозрительных на экстремумы.
Теорема.
Пусть
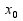 -внутренняя
точка Df,
V(
-внутренняя
точка Df,
V(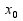 )
непрерывна и дифференцируема,
)
непрерывна и дифференцируема,
тогда
при переходе через
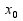 производная меняет знак с «+» на «-»
производная меняет знак с «+» на «-»
(«-» на
«+»),то
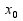 -
точка max(min).
-
точка max(min).
Д-во.
Для определенности предположим, что производная меняет знак с «+» на «-», тогда :
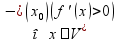 и
и
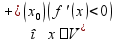 .
.
Рассмотрим
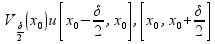 на
этих отрезках функции f
на
этих отрезках функции f
удовлетворяют условия возрастания и убывания соответственно, тогда
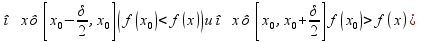
=>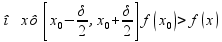
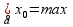
Данное условие верно для всех подозрительных на экстремумы точек.
Теорема. Достаточное условие экстремумов для стационарных точек
Пусть
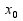 -внутренняя
точка области определения, которая
является стационарной.
-внутренняя
точка области определения, которая
является стационарной.
Пусть
в точке
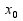 функция является дважды дифференцируемой,
функция является дважды дифференцируемой,
тогда
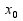 является точкой экстремума, причем
min(max),
если f”(
является точкой экстремума, причем
min(max),
если f”(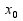 )>0(f”(
)>0(f”(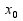 )<0).
)<0).
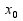 ∊Df
называется точкой наибольшего(наименьшего)
значения,
∊Df
называется точкой наибольшего(наименьшего)
значения,
если
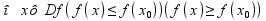 .
.
Если
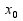 -
точка наибольшего(наименьшего) значения,
причем внутренняя,
-
точка наибольшего(наименьшего) значения,
причем внутренняя,
то она является точкой экстремума
Алгоритм нахождения наим(наиб) значения:
Находим все подозрительные на экстремумы точки ∊ отрезку
Вычисляем значение функции на концах отрезка и в найденных точках
Выбираем самое маленькое и самое большое значение