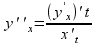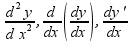
26. Производные высших порядков явно заданной функции

Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка. Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у"
(или f"(x),

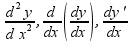
Итак, у"=(у')'. Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'

Производной n-го порядка (или n-й производной) называется производная от производной  (n-1) порядка: y⁽ⁿ⁾=(y^(n-1))¢ .

Производные порядка выше первого называются производными высших порядков.

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (у^ν или у⁽⁵⁾— производная пятого порядка).Пример 23.1

Найти производную 13-го порядка функции у=sinx.

Решение:

23.2.   Механический смысл производной второго порядка

Пусть материальная точка М движется прямолинейно по закону S=f(t). Как уже известно, производная S¢ _t равна скорости точки в данный момент времени: S'_t=V.

Покажем, что вторая производная от пути по времени есть величина, ускорения прямолинейного движения точки, т. е. S"=α.

Пусть в момент времени t скорость точки равна V, а в момент t+∆t — скорость равна V+∆V, т. е. за промежуток времени ∆t скорость изменилась на величину ∆V.

Отношение ∆V/∆t выражает среднее ускорение движения точки за время ∆t. Предел этого отношения при ∆t→0 называется ускорением точки М в данный момент t и обозначается буквой α:

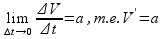
Но V=S'_t. Поэтому α=(S'_t)', т. е. α=S'_t'

3.3.   Производные высших порядков неявно заданной функции

Пусть функция у=ƒ(х) задана неявно в виде уравнения F(x;y)=0.

Продифференцировав это уравнение по х и разрешив полученное уравнение относительно у', найдем производную первого порядка (первую производную). Продифференцировав по х первую производную, получим вторую производую от неявной функции. В нее войдут х,у,у¢ . Подставляя уже найденное значение у' в выражение второй производной, выразим у" через х и у.

Аналогично поступаем для нахождения производной третьего (и дальше) порядка.Пример 23.2

 Найти у'", если х²+у²=1.

Решение: Дифференцируем уравнение х²+у²-1=0 по х: 2х+2у· у¢ =0.

Отсюда у'=-х/у. Далее имеем:

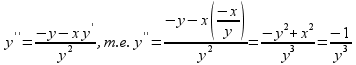
(так как х²+у²=1), следовательно,

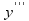
23.4. Производные высших порядков от функций, заданных параметрически

Пусть функция у=ƒ(х) задана параметрическими уравнениями

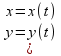
Как известно, первая производная у'х находится по формуле (23.1)

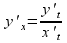
Найдем вторую производную от функции заданной параметрически. Из определения второй производной и равенства (23.1) следует, что