25. Дифференцируемость неявной функции, функции заданной параметрически. Примеры.

Пусть значения переменных х и у связаны уравнением F(x, y) = 0. (1) Если функция y = f(x), определенная на некотором интервале (а,в), такая, что уравнение (1) при подстановке в него вместо у выражения f(x) обращается в тождество, то говорят,

что уравнение (1) задает функцию y = f(x) неявно или что функция y = f(x) есть неявная функция. Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, то есть не представляя в виде y = f(x), так как часто это преобразование бывает технически сложным или невозможным. Для нахождения производной у'_х неявной функции, нужно продифференцировать по х обе части равенства (1),учитывая, что у есть функция от х. Затем из полученного

равенства. Пример:

Найти производную от функции, заданной неявно

 Навешиваем штрихи на обе части:
Используем правила линейности:
Находим производные:

Раскрываем все скобки:

Переносим все слагаемые с  в левую часть,

остальные – в правую часть:

В левой части выносим  за скобку:

Окончательный ответ: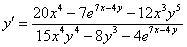

x = φ(t), y = ψ(t) В некоторой окрестности точки х0 пусть некоторая из этих ф-ий

например x = φ(t)непрерывна и строго монотонна в указанной окрестности,

тогда в этой окрестности для функции x = φ(t) существует обратная функция

t = φ(x) а в некоторой окрестности т. Х₀₌ φ(t₀) существует сложная функция

y = ψ(φ(x)) тогда y(x) называется параметрически заданной с помощью уравнений.

Теорема дифференцирования параметрически заданной ф-ии.