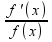;
x
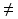0
=> (ln|x|)’={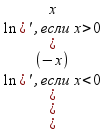
= {
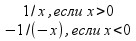. (ln|x|)’=1/x
(*) (u=f(x)-дифференцируемая
ф-я) и (теор. о производной сложной
ф-ии)=>(ln(f(x)))’=(*)
=
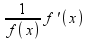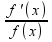Замечание: производная (ln(f(x)))’
называется логарифмической производной.
Чаще используется равенство
24. Логарифмическая дифференцируемость
Теор.:(логарифмическая производная) пусть u=f(x)-дифференцируемая ф-я, тогда имеет место равенство:
(ln
f)’=;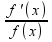
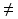x0
=> (ln|x|)’={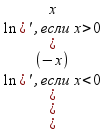
= {
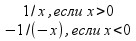. (ln|x|)’=1/x
(*) (u=f(x)-дифференцируемая
ф-я) и (теор. о производной сложной
ф-ии)=>(ln(f(x)))’=(*)
=
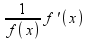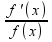Замечание: производная (ln(f(x)))’
называется логарифмической производной.
Чаще используется равенство
=
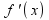f(x)(ln(f(x))’
(**) модуль опускается. Примечание: ф-ла
(**) применяется для нахождения производных
1)показательно-степенных ф-й 2)для нахождения дробей, содержащих большое число произведений и иррациональных
