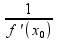в (.)x0,
тогда ф-я t=g(x)
также получит приращ.
,
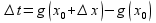тогда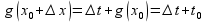
,
тогда ф-я f
получает приращение
.
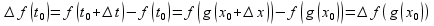Пусть f
дифферен. в (.)x0
и теор. о связи дифференцирования с
производной=>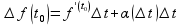
,
где
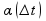-б.м23. Дифференцируемость сложной и обратной функций
Теор.1:(дифференцирование
сложных ф-й) пусть в некоторой окрестности
точки х0 для
U=f(t),
t=g(x0) существует
сложная ф-я f(g(x)),
пусть ф-я g
дифферен. в (.)x0,
ф-я f
дифферен. в (.)t0,
где t0=g(x0),тогда
сложная ф-я f(g(x))
дифферен. в (.)x0,
причем f’(g(x0))=
f’(t0)g’(x0)
док-во: придадим аргументу х произвольное
приращение
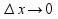в (.)x0,
тогда ф-я t=g(x)
также получит приращ.
,
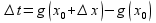тогда,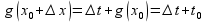
тогда ф-я f
получает приращение
.
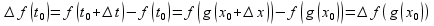Пусть f
дифферен. в (.)x0
и теор. о связи дифференцирования с
производной=>,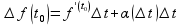
где
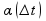-б.м
При
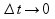(1). Ф-я дифферен. в (.)x0=>она
является непрерывной=> по определению
4 непрерывности: б.м. приращению аргумента
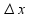соотв. б.м. приращение ф-ии
,
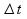т.е.
.
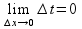Разделим равенство (1) на
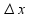и перейдем к пределу:
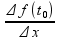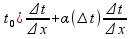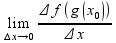=f’(
=>
=
f’(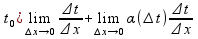
=>f’(g(x0))=f’(t0)g’(x0)+0
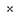g’(x0)=>
f’(g(x0))=f’(t0)g’(x0).
Теор.2:(производная обратной
ф-ии) пусть y=f(x)
определена и непрерыв на [а;b]
и имеет на нем обратную ф-ю x=g(y),
определенную на отрезке Y,
концами которого являются f(a)
и f(b).
Пусть x0-внутренняя
точка [а;b],
у0-внутренняя
точка отрезка Y,
причем x0=g(у0),
y0=t(x0).
Пусть в (.)x0
существует производная
ф-ии f’(x0)
0,
тогда в точке у0 существует
производная ф-ии g,
причем g’(у0)=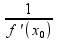
.
Док-во: придадим у0
приращение
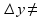0
т.к. g(y)-непрерывная
и монотонная ф-я (по теор. о существовании
обратной ф-ии), то приращение
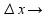0
при
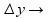0.
(g(у0))’=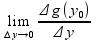
=
=
=
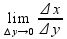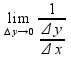