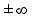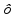 R
2) x=
х0, f’(х0)=
R
2) x=
х0, f’(х0)=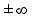 .
Док-во: 1)пусть f(x)-произвольная
(.)
касательной. к=tg
.
Док-во: 1)пусть f(x)-произвольная
(.)
касательной. к=tg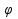 0=
f’(х0)-угловой
коэф. касател. f’(х0)
0=
f’(х0)-угловой
коэф. касател. f’(х0)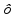 R,
М(x;y)-произвольная
(.)
касательной. Рассмотрим прямоугольный
треугольник М0МР:
tg
R,
М(x;y)-произвольная
(.)
касательной. Рассмотрим прямоугольный
треугольник М0МР:
tg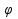 0=
0=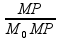 =
=21. Уравнения касательной и нормали к графику функции. Примеры
Теор.:
если ф-я имеет производную в (.)
х0, то в (.)
М0(х0;f(х0))
существует касательная вида 1) y=
f(х0)+
f’(х0)(x-х0),
f’(х0)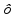 R
2) x=
х0, f’(х0)=
R
2) x=
х0, f’(х0)=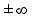 .
Док-во: 1)пусть f(x)-произвольная
(.)
касательной. к=tg
.
Док-во: 1)пусть f(x)-произвольная
(.)
касательной. к=tg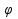 0=
f’(х0)-угловой
коэф. касател. f’(х0)
0=
f’(х0)-угловой
коэф. касател. f’(х0)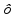 R,
М(x;y)-произвольная
(.)
касательной. Рассмотрим прямоугольный
треугольник М0МР:
tg
R,
М(x;y)-произвольная
(.)
касательной. Рассмотрим прямоугольный
треугольник М0МР:
tg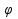 0=
0=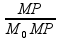 =
=
=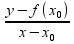 =>
f’(х0)=
=>
f’(х0)=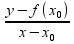 =>y=
f(х0)+
f’(х0)(x-х0).
2) f’(х0)=
=>y=
f(х0)+
f’(х0)(x-х0).
2) f’(х0)=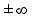 ,
тогда
,
тогда
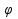 =90
=90 и касат. образует прямой угол с Ох и
имеет вид х=х0.
Прямая, которая проходит через точку
(х0;f(х0))
и перпендикулярна касательной в этой
точке – нормаль. Теор.:(ур-ние нормали)
ур-ние нормали имеет вид 1)y=
и касат. образует прямой угол с Ох и
имеет вид х=х0.
Прямая, которая проходит через точку
(х0;f(х0))
и перпендикулярна касательной в этой
точке – нормаль. Теор.:(ур-ние нормали)
ур-ние нормали имеет вид 1)y=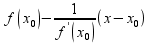 ,
f’(х)
,
f’(х)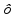 R/{0}.
2)y=y0,
f’(х)=
R/{0}.
2)y=y0,
f’(х)=