f(x0)=Ax+α(x)x,
где α(x)-б.м.
при
x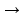
0,
то ф-я дифференцируема в (.)x0
, А-const.
Теор.: Дифференцируемость ф-ии в (.)x0
эквивалентна существованию конечной
производной. Док-во: пусть f
дифференц. в (.)x0
=> (1) =>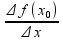
=А+α(x)=>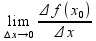
=
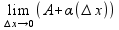=>20. Дифференцируемость. Правила дифференцируемости.
Если
приращение ф-ии представимо в виде (1)
f(x0)=Ax+α(x)x,
где α(x)-б.м.
при
x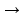0,
то ф-я дифференцируема в (.)x0
, А-const.
Теор.: Дифференцируемость ф-ии в (.)x0
эквивалентна существованию конечной
производной. Док-во: пусть f
дифференц. в (.)x0
=> (1) =>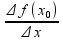=А+α(x)=>==>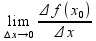
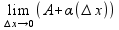=>f’(x0)=A-const=>f’(x0)
R.
пусть f’(x0)=AR=>(def)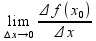=A=>(т.
О связи пределов с б.м.)
=
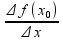A+α(x),
где
α(x)-б.м.=>f(x0)=
Ax+α(x)x(1)
чтд.
Из док-ва теор. вытекает,
что рав-во (1) можно записать в виде
f(x0)=
f`(x0)x+α(x)x,
α(x)-б.м.
при
x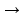0
(2). (1),(2)-тождества дифференцирцемости.
Теор.:(правила дифференцирования) Если
функции f и g дифференцируемы
в точке x0 то
в этой же точке также дифференцируемы
ф-ии (f+g),
fg, f/g (если g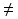
0) в
точке x0,
причем (f+g)'(x0)=
(f)'(x0)+(
g)'(x0),
(fg)'(x0)=
(f)'(x0)(
g)(x0)+
(f)(x0)(
g)'(x0),
(f/g)'(x0)=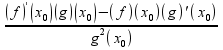
док-во: 2)f(x0)=
f(x0+х)-f(x0)*;
(fg)'(x0)=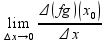
=
=
=
=(*)
=
=
=
=
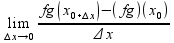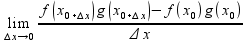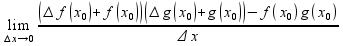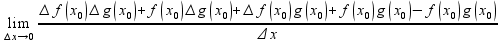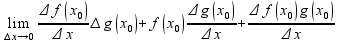=(**)(f)'(x0)
0+(f)(x0)(g)'(x0)+
(f)'(x0)(g)(x0)=
(f)'(x0)
(g)(x0)
+(f)(x0)(g)'(x0);
(**)-т.к. ф-я g
дифференц. в x0=>имеет
конечную производную=>непрерывна в
x0=>(опр.непрерывности)
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
ф-ии. чтд
