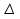 t]
тогда за
t]
тогда за
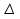 t
тело прошло
t
тело прошло
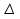 S(t0)=S(t0+
S(t0)=S(t0+
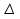 t)-S(t0)
тогда υcр=
t)-S(t0)
тогда υcр=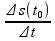 (средняя скорость)
(средняя скорость)19. Задачи, приводящие к понятию производной функции. Определение производной.
Зад.1:
Измерение мгновенной скорости. Рассмотрим
движение тела по прямой: пусть в момент
времени t
тело прошло путь s.
S(t)-ур-ние
движения тела. Зафиксируем момент врем.
t0
[t0;
t0+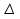 t]
тогда за
t]
тогда за
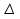 t
тело прошло
t
тело прошло
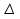 S(t0)=S(t0+
S(t0)=S(t0+
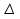 t)-S(t0)
тогда υcр=
t)-S(t0)
тогда υcр=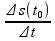 (средняя скорость)
(средняя скорость)
Чем меньше
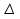 t,
тем точнее скорость в момент времени.
Мгновенной скоростью в момент времени
называется υмгн=
t,
тем точнее скорость в момент времени.
Мгновенной скоростью в момент времени
называется υмгн=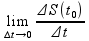
Зад.2: Касательная к кривой
рассмотрим
ф-ю f(x)
обозначим Гf
ее график 
зафиксир. на графике (.)М0(х0;f(х0)) M(х;f(х))-произвольная (.)графика, М0 М-секущая,
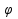 -угол,
образованный секущей с положительным
направлением оси Ox,
будем устремлять M
к фиксированной М0,
двигая ее по графику, тогда секущая
займет предельное положение касательной
в (.)х0,
-угол,
образованный секущей с положительным
направлением оси Ox,
будем устремлять M
к фиксированной М0,
двигая ее по графику, тогда секущая
займет предельное положение касательной
в (.)х0,
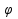 0-
угол между касательн. и положительным
направлением Ox.
Если существ. конечный предел
0-
угол между касательн. и положительным
направлением Ox.
Если существ. конечный предел
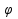 при
при
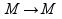 0
0 Гf,
существ. касательная(прямая с угловым
коэф. к0=tg
Гf,
существ. касательная(прямая с угловым
коэф. к0=tg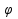 0).
Найдем угловой коэф. касательной,
рассмотрим прямоуг. треуг. М0
МК.
0).
Найдем угловой коэф. касательной,
рассмотрим прямоуг. треуг. М0
МК.
М0
К=
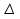 х,
х,
МК=
f(х0+
х)- f(х0)=
f(х),
тогда к=tg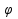 =
=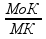 =
=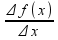 ,
перейдя к пределам получ.: к0=
,
перейдя к пределам получ.: к0=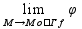 =
tg
=
tg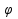 0;
tg
0;
tg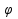 0=
0=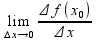 ;
к0= tg
;
к0= tg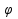 0=
0=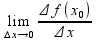
Опр.:
пусть f(x)
определ на Df
x0 Df,
тогда
Df,
тогда
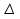 x=x-x0
называется приращением
аргумента, тогда
x=x-x0
называется приращением
аргумента, тогда
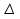 f(x0)=
f(x0+
f(x0)=
f(x0+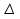 х)-
f(x0)
называется приращением ф-ии в (.)х0.
Если существ. предел отношения приращения
ф-ии в (.)х0
к приращению аргумента, когда последнее
стремится к 0, т.е.
х)-
f(x0)
называется приращением ф-ии в (.)х0.
Если существ. предел отношения приращения
ф-ии в (.)х0
к приращению аргумента, когда последнее
стремится к 0, т.е.
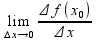 ,
то он называется производной ф-ии в
(.)х0.
,
то он называется производной ф-ии в
(.)х0.
f’(x0)=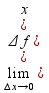 0)=
0)=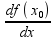 Замечание.: в указ. определении. Предел
может принимать знач. +
Замечание.: в указ. определении. Предел
может принимать знач. +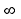 ,
-
,
-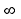 ,
,
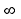 ,
так же не всякая ф-я может иметь производную
и не во всякой точке.
,
так же не всякая ф-я может иметь производную
и не во всякой точке.