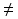 0 ,
то на концах по крайней мере одного из
частичных отрезков функция f принимает
значения разных знаков.
0 ,
то на концах по крайней мере одного из
частичных отрезков функция f принимает
значения разных знаков.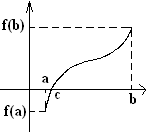
17. Общие свойства функций, непрерывных на отрезке. Теоремы Больцано-Коши
Первая теорема Больцано-Коши. Пусть f непрерывна на [a,b] и на концах отрезка принимает значения разных знаков, т.е. f(a)f(b)<0. Тогда существует точка с принадлежащяя (a,b) такая, что f(c)=0.
Док-во:
Разделим отрезок [a;b] точкой х=a+b/2
на
2 равных отрезка, если f(х)=0 ,
то теорема доказана , если же f(х)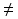 0 ,
то на концах по крайней мере одного из
частичных отрезков функция f принимает
значения разных знаков.
0 ,
то на концах по крайней мере одного из
частичных отрезков функция f принимает
значения разных знаков.
Обозначим
этот отрезок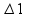 .
разбиваем точкой х1
на
две равные части. Если f(х1)=0 ,
то теорема доказана, если же
f(х)
.
разбиваем точкой х1
на
две равные части. Если f(х1)=0 ,
то теорема доказана, если же
f(х)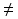 0 ,
на некотором k∈N
шаге будем
иметь f(хk)=0 и
тогда теорема доказана , или получаем
систему стягивающих отрезков
0 ,
на некотором k∈N
шаге будем
иметь f(хk)=0 и
тогда теорема доказана , или получаем
систему стягивающих отрезков
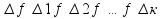 ,длинны
которых стремятся к 0,при к
,длинны
которых стремятся к 0,при к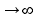 .
.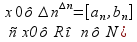 ^x0=
^x0=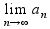 =
=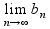 .по
построению отрезков получаем f(
.по
построению отрезков получаем f(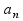 )
f(
)
f(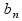 )<0(*)
)<0(*)
f(x)
непрерывная на отр [a,b]=>∀n∈N(f(x)
непрерывна на
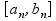 =>(по(*))
=>(по(*))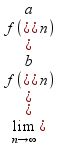 =>(свойства
пределов функции)f
=>(свойства
пределов функции)f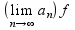 (
(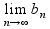 )≤0=>f(x0)f(x0)≤0=>f2(x0)≤0<=>
f2(x0)=0<=>f(x0)=0=>∃c=x∈(a,b)(f(c)=0).
)≤0=>f(x0)f(x0)≤0=>f2(x0)≤0<=>
f2(x0)=0<=>f(x0)=0=>∃c=x∈(a,b)(f(c)=0).
Следствие.(о корне алгебраических уравнений не чётной степени).Любое уравнение нечётной степени имеет хотя бы 1 корень.
Вторая
теорема Больцано – Коши(о промежуточном
значении непрерывной функции)/пусть
F(X)непрерывна
на [a,b].f(a)=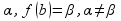 .тогда
любое значение
.тогда
любое значение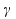 между
между
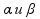 f(x)
принимает хотя бы в 1 точке с
f(x)
принимает хотя бы в 1 точке с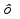 (а,b).Док-во:пусть
для определенности
(а,b).Док-во:пусть
для определенности
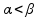 ,тогда
по аксиоме непрерывности
,тогда
по аксиоме непрерывности ).рассмотрим
).рассмотрим
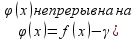 [a,b])^(
[a,b])^(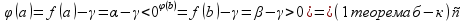 с
с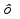 (а,b)(
(а,b)(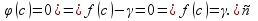 с
с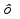 (а,b)(
(а,b)(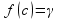 )
)
Следствие: Если f(x) определена и непрерывна в каком-либо промежутке Х, то принимаемые ею значения так же заполняют некоторый промежуток.