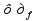 ,если
выполняется одно из эквивалентных
условий:
,если
выполняется одно из эквивалентных
условий:14.Определение непрерывности функции в точке. Свойства непрерывных функций
О:
Функция f(x)
называется непрерывной в точке х0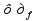 ,если
выполняется одно из эквивалентных
условий:
,если
выполняется одно из эквивалентных
условий:
2.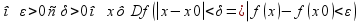
3.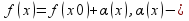 б.м.
при х
б.м.
при х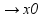
4.если
б.м. приращению аргумента
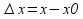 соответствует
б.м. приращение функции
соответствует
б.м. приращение функции
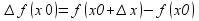 ,т.е.
,т.е.
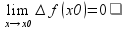
Докажем эквивалентность 1 и 4 условия:
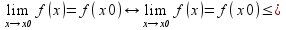 (над
значком х=х0+
(над
значком х=х0+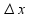 )
)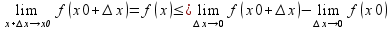 =0
=0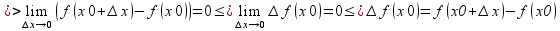 ,т.е.
,т.е.
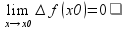
Если хотя бы одно из условий 1-4 нарушается,то говорят,что функция f(x) терпит разрыв в точке х0.
А х0- точка разрыва
О: Функция f(x) называется непрерывной в точке х0 справа(слева)если:
Lim
x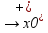 f(x)=f(x0)
lim x
f(x)=f(x0)
lim x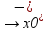 f(x)=f(x0)
f(x)=f(x0)
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций
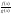 –
есть непрерывная функция при
условии, что g(x)
не равна нулю в точке х0.
–
есть непрерывная функция при
условии, что g(x)
не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если f(x)непрерывна в т.х0 , g(x) – непрерывна в точке у0=f(x0) , то функция g(f(x)) – тоже непрерывная функция точке x0.
Док-во:
g(y)
непр. в у0(и f(x)
непр.в точке х0)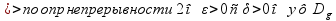 (|y-y0|<
(|y-y0|<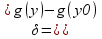 |<
|<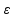 )
^
)
^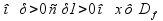 (|x-x0|<
(|x-x0|<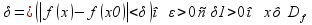 (|x-x0|<
(|x-x0|<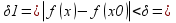 |y-y0|<
|y-y0|<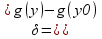 |<
|<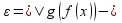 g(f(x0))|<
g(f(x0))|<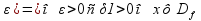 (|x-x0|<
(|x-x0|<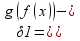 g(f(x0))|<
g(f(x0))|<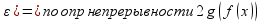 -непрерывна
в точке х0.
-непрерывна
в точке х0.
Все рассмотренные выше элементарные функции непрерывны к каждой точке своей области определения.
Док-во:
Пусть х0 произвольно взятая f(х)=sin х
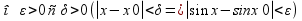 (*)
(*)
Для
фиксированного
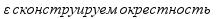 в
точке х0 такую,что для всех толчек из
этой окрестности значение функции
удовлетворяет неравенству (*)
в
точке х0 такую,что для всех толчек из
этой окрестности значение функции
удовлетворяет неравенству (*)
|sinx-sinx0|<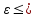 |2sin
x-x0/2
cos
x+x0/2|<
|2sin
x-x0/2
cos
x+x0/2|<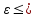 |2sin
x-x0/2
|<
|2sin
x-x0/2
|<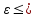 2
x-x0/2|<
2
x-x0/2|<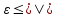 x-x0|<
x-x0|<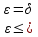 )|x-x0|<
)|x-x0|<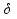 .
.