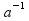
R
(a*
R
(a*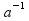 =
=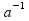 *a=1)
*a=1)1.Аксиоматическое определение мн-ва действительных чисел . Св-во полноты.
Опр. Мн-во R назыв. Мн-ов действительных (вещественных) чисел,а его элементы действ-ми числами,если
выполняются след. аксиомы:
1)аксиомы сложения: А0: a,b R !с R (a+b=c)
A1: a,b,с R (a+(b+c)=(a+b)+c)
A2: 1) 0 R a (a+0=0+a)
2) a R -a R (a+(-a)=(-a)+a=0)
A’1: : a,b R (a+b=b+a)
2) аксиомы умножения: М0: a,b R !с R (a*b=c)
М1: a,b,с R (a*(b*c)=(a*b)*c)
М2: 1) 1 R a R (a*1=1*a)
2)
a
R
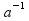
R
(a*
R
(a*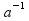 =
=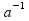 *a=1)
*a=1)
М’1: : a,b R (a*b=b*a)
3) связь 1-2.аксиома дистрибутивности: D1: a,b,с R (a*(b+c)=a*b+a*c)
4)аксиомы порядка: П1: a R (а≤a)(рефлексивность)
П2: a,b R ((a≤b)^(b≤a)=>a=b(антисимметричность)
П3: a,b,с R((a≤b)^(b≤c)=>(a≤c)(транзитивность)
П4: a,b R((a≤b)v(b≤a))(линейная упорядочность)
П5: a,b,с R((a≤b)=>((a+c)≤(b+c))(связь сложения и порядка)
П6 a,b,с R((0≤а)^(0≤b)=>(0≤a*b))(связь умножения и порядка)
5)аксиомы полноты(непрерывности): H1: A,B ⊂R ^A,B≠⊘aR^b R(a≤b) E R(a ≤E ≤b)
Пусть Х-непустое,ограниченное сверху(снизу) мн-во.В(Н)-мн-во всех верхних(нижних) граней,тогда
b
R(xX(x b)^
b’B(b≤b’)
bH(xX(x≥b)^b’B(b’≤b)
b)^
b’B(b≤b’)
bH(xX(x≥b)^b’B(b’≤b)